/fdata%2F0416819%2Favatar.png){kind=avatar}
19 septembre 2006
2
19
/09
/septembre
/2006
17:30
Dans une des conférences prononcées en 1983 à l'Université de Californie à Los Angeles (UCLA) en mémoire d'Alix Mautner, Feynman illustre le principe de moindre temps en reprenant une analogie cinématique de la réfraction qu'il avait déjà exposée 20 ans auparavant (analogie devenue célèbre bien que sexiste, célèbre parce que sexiste : n'oublions pas que son premier public était un amphitéâtre de garçons de la Caltech !) :
« Il se trouve que la lumière se propage moins vite dans l'eau que dans l'air (...) ; de ce fait, un trajet dans l'eau "coûte plus cher" que le même trajet dans l'air. Il est facile de voir quel sera dans ces conditions le trajet de moindre temps. Imaginez que vous soyez un maître-nageur chargé de la sécurité d'une plage. Vous êtes en S et tout à coup, vous apercevez une jolie fille en train de se noyer en D (Fig. 1) [Cours de 1961-1962 : «imaginons qu'une jolie fille soit tombée d'un bateau, et qu'elle appelle au secours dans l'eau au point D. Nous sommes au point A sur la terre et nous voyons l'accident, or nous savons courir et également nager» : entre '61-62 et '83 le bateau a disparu et "nous" est devenu maître-nageur ; une chose demeure cependant : la fille, qui se doit d'être «jolie» pour donner une raison supplémentaire et égoïste au sauveteur de sauver et à l'auditeur mâle d'écouter]. Comment faire pour la sauver, sachant que vous courez plus vite sur le sable que vous ne nagez dans l'eau ?
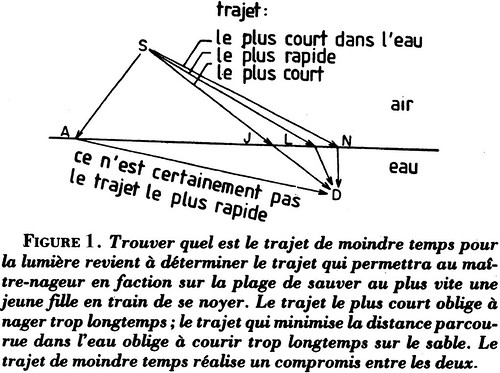
Le problème revient à déterminer l'endroit où vous devez entrer dans l'eau de manière à atteindre le plus tôt possible la malheureuse en train de se noyer. Il ne vous viendra évidemment pas à l'idée de vous précipiter au plus vite dans l'eau, en A, pour devoir ensuite nager comme un fou de A à D. Faut-il alors se diriger en ligne droite vers la victime, c'est-à-dire entrer dans l'eau en J ? Non ; ce chemin-là non plus n'est pas celui qui prend le moins de temps. Évidemment, on imagine mal qu'un sauveteur se mette à calculer le chemin de moindre temps avant de se porter au secours de la jeune fille. Cependant, il est possible, de fait, de calculer le point d'entrée dans l'eau qui rend le temps de parcours minimal. Ce trajet correspond à un compromis entre la ligne droite (passant par J) et le parcours qui rend minimale la distance dans l'eau (passant par N). Il en va ainsi pour la lumière : elle emprunte le trajet qui, la faisant entrer dans l'eau en un point, disons L, situé entre J et N, correspond au moindre temps. »Richar Feynman, Lumière et matière, Une étrange histoire,
trad. par Françoise Balibar et Alain Laverne,
Paris, InterEditions, 1987 (éd. de poche Points Sciences S86, 206 p., p. 76-77)
Comme il s'agit d'une conférence, Feynman ne démontre pas sa dernière affirmation.
Mais vous, chers petits sacrabées, vous êtes en âge non seulement de comprendre la démonstration mais de l'établir.
A vos crayons donc ! Justifiez l'affirmation de Feynman (Il en va ainsi pour la lumière) en exprimant la condition pour que le temps de sauvetage soit minimum.
Un énoncé plus scolaire du problème et la réponse au billet d'optique suivant.
Mais vous, chers petits sacrabées, vous êtes en âge non seulement de comprendre la démonstration mais de l'établir.
A vos crayons donc ! Justifiez l'affirmation de Feynman (Il en va ainsi pour la lumière) en exprimant la condition pour que le temps de sauvetage soit minimum.
Un énoncé plus scolaire du problème et la réponse au billet d'optique suivant.
Partager cet article
